Grundlagen der 3D Animation
First things first!
Wie schafft es eine Maschine, die nur mit Nullen und Einsen arbeitet, Bilder und Filme zu erstellen? Bis zu unserem heutigen Leistungsstand war es ein langer Weg. Bereits in den 60er Jahren erstellten Wissenschaftler die ersten Bilder mit Hilfe eines Computers. In den folgenden Jahrzehnten kamen ständig neue Technologien hinzu. Diese machten die Darstellung von 3D Grafiken immer besser, realistischer oder auch künstlerischer. Die Grundbegriffe und Techniken dazu möchte ich hier kurz beschreiben.
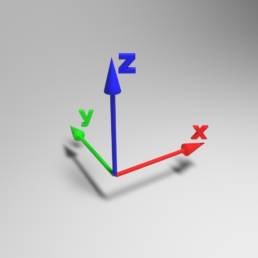
Die dritte Dimension
3D steht als Kürzel für 3 Dimensionen.
Diese werden als X Achse für die horizontale , Y Achse für die vertikale und die Z-Achse für die Tiefe bezeichnet.
In 3D Grafiken werden Punkte und Objekte im Raum durch diese drei Werte definiert. Diese Technik bildet die Grunlagen für 3D Grafiken.
Als Beispiel würde ein Würfel mit der Kantenlänge 1 folgendermaßen gespeichert werden
[0,0,0]-[1,0,0]-[0,1,0]-[1,1,0]-[0,0,1]-[1,0,0]-[0,1,1]-[1,1,1].
Das ist vielleicht etwas verwirrend, soll aber nur aufzeigen, wie komplex die Berechnungen innerhalb einer 3D Grafik sind.
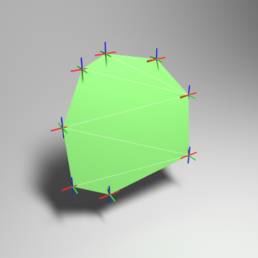
Poligon
‘Poli-gon’ steht für ‘Viel-eck’ und bezeichnet eine geometrische Figur, die aus mehreren Ecken besteht
und idealerweise auf einer Ebene liegen.
Poligone sind die “Grundbausteine” der 3D Grafik. Alle Objekte bestehen aus Poligonen. Je mehr Poligone
ein Objekt hat, desto realistischer ist es darzustellen. Mit der steigenden Zahl der Poligone steigt aber auch der Rechenaufwand
für den Computer und somit die Zeit bis ein Bild fertig gerendert ist.
Eine Sonderform unter den Poligonen für 3D Grafik haben die Dreiecke.
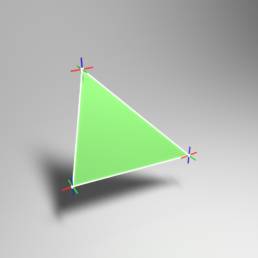
Poligone: Dreieck
Das Dreieck oder Trigon ist die Elementarform in der 3D Grafik. Es stellt die Grundlage für alle 3D Grafiken dar.
Es ist die einfachste Form, die erstellt werden kann. Ein Eckpunkt / Vertex weniger und es wäre nur eine Linie (Nichts gegen Linien).
Alle Objekte in der 3D Grafik werden durch Dreiecke dargestellt, vom einfachen Würfel, bis zum Monster aus den Hollywood Filmen.
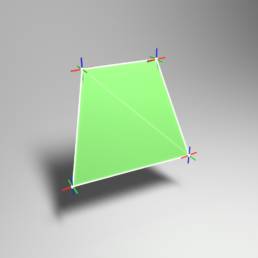
Quads
Auch wenn Dreiecke die Basis für 3D Grafiken darstellen, so werden die meisten Modelle oder Objekte aus sogenannten Quads, also Rechtecken gebaut. Diese bestehen aus 2 Dreiecken, welche flach aneinander liegen.
Es gibt viele Gründe für das modellieren mit Quads, einer ist davon z.B. die Möglichkeit mit einem Klick das Grundgitter eines Models höher aufzulösen, das sogenannte Tesselieren.
Ein anderer Vorteil sind die guten Eigenschaften von Quads bei der Animation von organischen Oberflächen.
Oft muss an Objekten ein sogenannter Re-Topologie Prozess durchgeführt werden, wobei die gesamte Oberfläche mit Quads neu modelliert wird.

Farbtiefe
Computergrafiken können nur eine begrenzte Anzahl von unterschiedlichen Farben enthalten.
Die Farben werden als sogenannte RGB Werte gespeichert, RGB steht für Rot-Grün-Blau, den einzelnen Farbkanälen.
Die Farbtiefe bestimmt wie viele Abstufungen jedem Kanal zur Verfügung stehen. Da Prozessoren Werte in Bits speichern, also entweder als Nullen oder Einsen bzw. An oder Aus, ergibt sich aus der Menge der Bits eine Zahl die gröbere oder feinere Abstufungen pro Kanal ermöglicht.
Bei einem Bit lässt sich bespielsweise nur Weiss oder Schwarz darstellen. Bei zwei Bit hat man schon vier Abstufungen. Am weitesten verbreitet sind 8-Bit Grafiken, bei denen 256 Abstufungen möglich sind.


Motion Blur
Bewegungsunschärfe ist eine Eigenschaft von real gefilmtem Material.
Indem sich ein Objekt während der Belichtungszeit bewegt, wird es verwischt aufgezeichnet.
Was vielleicht als zu vermeidendes Manko erscheint, ist jedoch notwendig für eine angenehme Betrachtung von Videos , da andernfalls ein sogenannter Shutter Effekt auftritt, der eher als störend empfunden wird.
Die digitale Berechnung von Motion Blur ist aufwendig und erfordert ein vielfaches an Rechenzeit, da ein Einzelbild in mehrere Unterbilder aufgeteilt werden muss, die dann übereinander gelegt werden.

Partikelsysteme
Für Situationen in denen hunderte oder tausende Objekte benötigt werden die gemeinsame Verhaltensweisen haben, nutzt man sogenannte Partikelsysteme.
Einsatzbereiche sind bespielsweise: Schneeflocken, Schwebeteilchen, Insektenschwärme, Geröllbrocken usw.
Einem Partikelsystem wird ein bestimmter Satz an Regeln und Konditionen zugewiesen, welche dann für die generierte Anzahl aller Partikel in dem System gilt.
Regeln und Konditionen können fast alles sein, von Schwerkraft, Geschwindigkeit, Anziehungs und Abstossungskräften bis zu Lebensdauer und Aussehen.

Texturen
Mit Texturen werden Objekte eingefärbt oder mit Bildern belegt.
Es gibt viele Arten der Texturierung, Objekte können umwickelt oder flächig belegt werden.
Je nach Situation sind unterschiedliche Arten der Texturierung nötig.
Ein Würfel benötigt z.B. 6 flache Texturen, eine Erdkugel wie im Beispielbild,
braucht ein schon vorher verzerrtes Bild um korrekt dargestellt zu werden.

Spezielle Texturen
Eine einfache Textur reicht oft nicht aus, um ein Objekt glaubhaft oder fotorealistisch
darzustellen. Meistens nutzt man Kombinationen unterschiedlicher Oberflächeneigenschaften.
Im Beispiel links besteht die Erdkugel aus 3 Texturen die gemeinsam das Modell bilden.
Es gibt die Bitmap Grafik, welche die Farben definiert, eine Specular Map, welche Reflektionen steuert
und eine sogenannte Displacement Map die Erhebungen und kleine Details darstellt.

Die dritte Dimension
3D steht als Kürzel für 3 Dimensionen.
Diese werden als X Achse für die horizontale , Y Achse für die vertikale und die Z-Achse für die Tiefe bezeichnet.
In 3D Grafiken werden Punkte und Objekte im Raum durch diese drei Werte definiert. Diese Technik bildet die Grunlagen für 3D Grafiken.
Als Beispiel würde ein Würfel mit der Kantenlänge 1 folgendermaßen gespeichert werden
[0,0,0]-[1,0,0]-[0,1,0]-[1,1,0]-[0,0,1]-[1,0,0]-[0,1,1]-[1,1,1].
Das ist vielleicht etwas verwirrend, soll aber nur aufzeigen, wie komplex die Berechnungen innerhalb einer 3D Grafik sind.
